[最も人気のある!] 連続する整数の和 証明 155414-連続する整数の和 証明
問題 90を連続する自然数の和で表す方法は何通りあるか。 出典:マスターオブ整数 読者になる 短くて面白い数学の問題コレクション ~シンプルな難問~ スポンサーリンク 1412
連続する整数の和 証明- 丁寧に証明するならば、①では余りによる分類を利用して、 (1) のとき、 (積) で の倍数 (2) のとき (積) で の倍数 となります。 同様に②も で場合分けすれば証明できます。 なお③につ 3 3 つの連続する整数の和は 3 3 の倍数になる。 中 1 数学の中間・期末試験ではこの命題の証明問題がよく出ます。 証明に入る前に、命題が正しいことを確認しましょう。 「 3 3 つの
連続する整数の和 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 | ||
 |  |  |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
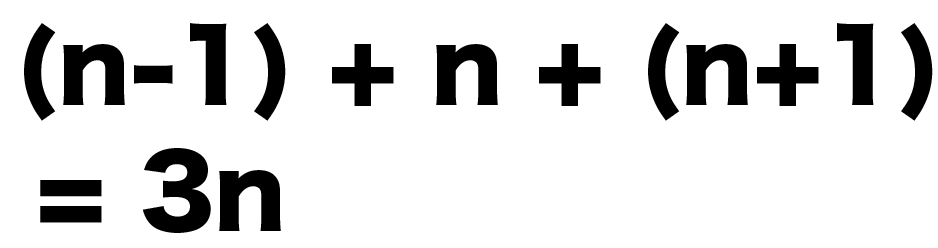 |  |  |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 | ||
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
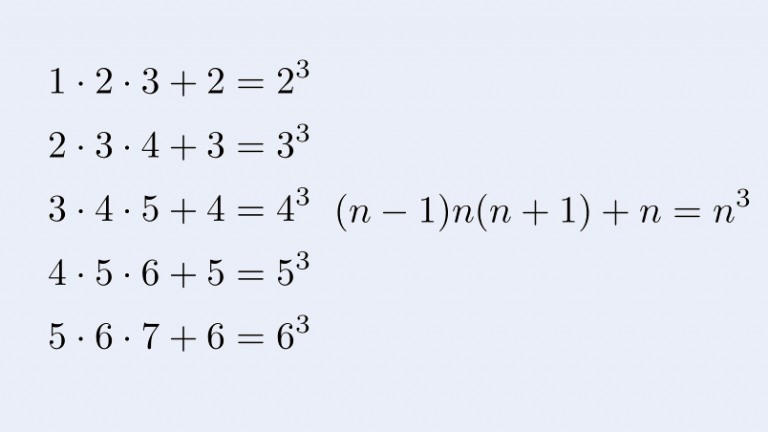 |  | |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
そう。整数の性質。たとえば,5,6 とか,9,10 とか考えると,連続する 2 つの整数のどっちかは必ず偶数だから,その積は偶数,つまり 2 の倍数になる。以下では,上記の定理を3つの方法で証明します。 整数論のルジャンドルの定理を用いる素直な方法 二項係数の意味を考える方法 二項係数と数学的帰納法を用いる方法 ※ただし,連続する n n 個の
Incoming Term: 連続する整数の和 証明,
コメント
コメントを投稿